Features

Base types

Sparkground has an infinite family of base types, each written as a symbol where a type is expected. For instance, in (let (((x Foo) ·)) ·), the binding x is annotated with base type Foo.

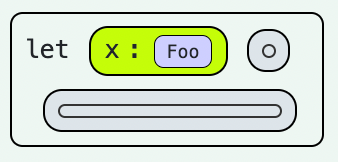
Some base types have special built-in behaviour.

• Values of the following base types are created by literal syntax:
  • Boolean
  • Integer
  • Number
  • String
  • Symbol
• Top and bottom types (see subtyping):
  • Any is the top type
  • Never is the bottom type
• Gradual typing:
  • ? is the “unknown” type
• Produced and consumed by built-in functions:
  • Empty (empty list, used as a “null” type)
  • Graphic (describes something that can be drawn to the screen)

Type constructors

Sparkground supports type constructors, which are (uninterpreted) functions that operate on types to construct new types. Like with base types, any symbol written where a type constructor is expected (such as (type (Here ·)), where type is syntax that denotes a type expression ¹) will be treated as one. In practice, all useful type constructors are built-in, as there is currently no pleasant interface for users to define their own.

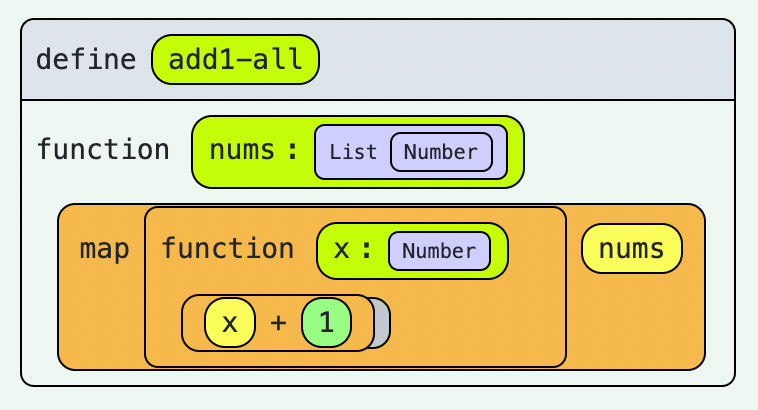
List is a type constructor that takes one type parameter—say X—where (List X) denotes lists of objects of type X. Lists are core to the language and can be created with literal syntax. (In fact, like Scheme, expressions are syntactically just nested lists.) Note that at runtime, lists may be hetergeneous, such as (1 two "three"). The best static type for heterogeneous lists in the current system is (List J), where J is the join ($\vee$) of the types in the list. As the current system does not support union types, J usually ends up as Any, the top type. (But see type join and meet for the complete definition.)

Other built-in type constructors relate to function types:

• $(\texttt{Function}\ \ \texttt{Arg}_1\ \ \ldots\ \ \texttt{Arg}_n\ \ \texttt{Result})$ is the type of (fixed-arity) functions from $\texttt{Arg}_1\ \ \ldots\ \ \texttt{Arg}_n$ to $\texttt{Result}$.

  The type constructor Function takes an arbitrary positive number of type parameters—conceptually, it is overloaded with the infinite overload set $\{\, \texttt{Function}/n \mid n \in \mathbb{N} \,\}$, where $(\texttt{Function}/n\ \ \texttt{Arg}_1\ \ \ldots\ \ \texttt{Arg}_n\ \ \texttt{Result})$ is the type of functions with arity $n$.

• $(\texttt{Function*}\ \ \texttt{Arg}_1\ \ \ldots\ \ \texttt{Arg}_n\ \ \texttt{Result})$ is the type of variadic functions from $\texttt{Arg}_1\ \ \ldots\ \ \texttt{Arg}_{n-1}$, and zero or more $\texttt{Arg}_n$, to $\texttt{Result}$.

  Like Function, Function* is conceptually overloaded, with the overload set $\{\, \texttt{Function*}/n \mid n \in \mathbb{N}, n > 0 \,\}$.

  The last argument type is treated as optional and infinitely repeatable (like a Kleene star). More concretely, $(\texttt{Function*}/n\ \ \texttt{Arg}_1\ \ \ldots\ \ \texttt{Arg}_n\ \ \texttt{Result})$ is modeled by the infinite intersection type $\bigcap_{m \in \mathbb{N}} (\texttt{Function*}/n\ \ \texttt{Arg}_1\ \ \ldots\ \ (\texttt{Arg}_n)^m\ \ \texttt{Result})$.

For example:

• string-repeat has type (Function String Integer String), which pretty-prints as (String Integer → String)
• string-concatenate has type (Function* String String), which pretty-prints as (String... → String).

Parametric polymorphism

Parametric polymorphism is the ability to endow an expression with an infinite family of types by allowing type constructor parameters to vary by usage. For example, $(\forall\texttt{\#E}.\ \ \texttt{\#E} \to (\texttt{List}\ \ \texttt{\#E}))$ is the type of values that, for every possible substitution of $\texttt{\#E}$, can be treated as a function from $\texttt{\#E}$ to $(\texttt{List}\ \ \texttt{\#E})$. Such types are polymorphic, generic, or universally quantified. Values of this type include $(\lambda \texttt{x}.\ \ (\texttt{list}))$ and $(\lambda \texttt{x}.\ \ (\texttt{list}\ \ \texttt{x}\ \ \texttt{x}))$.

In Sparkground, the special syntax $(\texttt{All}\ \ (\texttt{\#X}_1 \ldots \texttt{\#X}_n)\ \ \texttt{T})$ names a universally quantified type $\texttt{T}$, which can refer to the bound type parameters $\texttt{\#X}_1,\;\ldots,\;\texttt{\#X}_n$. For example, the built-in cons function has type (All (#E) (Function #E (List #E) (List #E))).

Sparkground has impredicative polymorphism: it admits $\forall$ types in contravariant position, and type variables can be instantiated to $\forall$ types.

Subtyping

Subtyping rules define which types can be correctly assigned to each other. When $\texttt{T} <: \texttt{U}$ ($\texttt{T}$ is a subtype of $\texttt{U}$), every expression of type $\texttt{T}$ can also be treated as having type $\texttt{U}$; hence, assigning an expression of type $\texttt{T}$ to an annotated binding of type $\texttt{U}$ is allowed.

The subtyping relation is reflexive. To ensure this for certain simple cases, we start with the following two rules:

• $\texttt{B} <: \texttt{B}$ for every base type $\texttt{B}$
• $\texttt{X} <: \texttt{X}$ for every type variable $\texttt{X}$

Next, we add rules that introduce top and bottom types. $\texttt{Any}$ is the top type, so everything can be assigned to it:

• $\texttt{T} <: \texttt{Any}$ for every type $\texttt{T}$

$\texttt{Never}$ is the bottom type, so it can be assigned to anything:

• $\texttt{Never} <: \texttt{T}$ for every type $\texttt{T}$

Expressions typeable as $\texttt{Never}$ will never produce a value, hence the name.

Subtyping rules that relate types with different tags are referred to as nominal. Built-in nominal rules are:

• $\texttt{Integer} <: \texttt{Number}$
• $\texttt{Empty} <: (\texttt{List}\ \ \texttt{T})$ for every type $\texttt{T}$

The rest of the subtyping rules are structural, relating types built from the same type constructors. To enable this, each type constructor has an associated variance signature, such as $(\texttt{C}\,-\,-\,+)$. In general, if $\texttt{C}$ is given $n$ parameters as a type constructor, parameter $i \in [1..n]$ of $\texttt{C}$ has variance $v(\texttt{C}, i) \in \{\, +,\, -,\, 0 \,\}$, corresponding to covariance, contravariance, and invariance, respectively.

Some built-in type constructors have variance signatures:

• $(\texttt{List}\ \ +)$
• $(\texttt{Function}\ \ [-\ \cdots]\ \ +)$
• $(\texttt{Function*}\ \ [-\ \cdots]\ \ +)$

All other type constructors are invariant in every position. (This could be amended in the future for user-defined type constructors.)

With type parameter variance in place, the schema for structural subtyping rules is:

• $(\texttt{C}\ \texttt{T}_1\ \cdots\ \texttt{T}_n) <: (\texttt{C}\ \texttt{U}_1\ \cdots\ \texttt{U}_n)$ if $\texttt{T}_i\ {\footnotesize{<:>}}_{v(\texttt{C},\,i)}\ \texttt{U}_i$ for all $i \in [1..n]$

$\texttt{T}\ {\footnotesize <:>_s}\ \texttt{U}$ can be read as $\texttt{T}$ and $\texttt{U}$ are compatible according to the variance sign $s$. It is the smallest relation such that:

• $\texttt{T}\ {\footnotesize <:>}_{+}\ \texttt{U}\$ if $\ \texttt{T} <: \texttt{U}$ [covariant];
• $\texttt{T}\ {\footnotesize <:>}_{-}\ \texttt{U}\$ if $\ \texttt{U} <: \texttt{T}$ [contravariant];
• $\texttt{T}\ {\footnotesize <:>}_{0}\ \texttt{U}\$ if $\ \texttt{T} = \texttt{U}$ [invariant].

For example, $(\texttt{Function}\ \ \texttt{Number}\ \ \texttt{Integer}) <: (\texttt{Function}\ \ \texttt{Integer}\ \ \texttt{Number})$, since:

• Both are unary function types, built from type constructor $\texttt{Function}/1$;
• $\texttt{Function}/1$ is contravariant in its parameter type and covariant in its return type, i.e., $$v(\texttt{Function}/1, i) = \begin{cases} \ - &\text{if } i ≤ 1 \\ \ + &\text{if } i = 2\,; \end{cases}$$
• $\texttt{Integer} <: \texttt{Number}$, so $\texttt{Number}\ {\footnotesize <:>}_{-}\ \texttt{Integer}$, and $v(\texttt{Function}/1, 1) = -$;
• $\texttt{Integer} <: \texttt{Number}$, so $\texttt{Integer}\ {\footnotesize <:>}_{+}\ \texttt{Number}$, and $v(\texttt{Function}/1, 2) = +$.

Finally, universally quantified types are related when they bind the same variables and their body types are related:

• $\forall \overline{\texttt{\#X}}.\ \texttt{T} <: \forall \overline{\texttt{\#X}}.\ \texttt{U}\$ if $\ \texttt{T} <: \texttt{U}$.

This rule alone is sound, but does not admit much flexibility. An assignment of $(\lambda\ (x)\ x)$ to a binding of type $(\forall \texttt{\#X}.\ \texttt{\#X} \to \texttt{\#X})$ fails to typecheck, because $(\lambda\ (x)\ x) : \texttt{?} \to \texttt{?}$ cannot be polymorphically generalized. This is a known deficiency. Fixing it, with the new syntax, UI, and typing rules that entails, falls under future work. (Parametric polymorphism exists in Sparkground primarily to ease working with built-in functions like map and list, which does work with the current rules.)

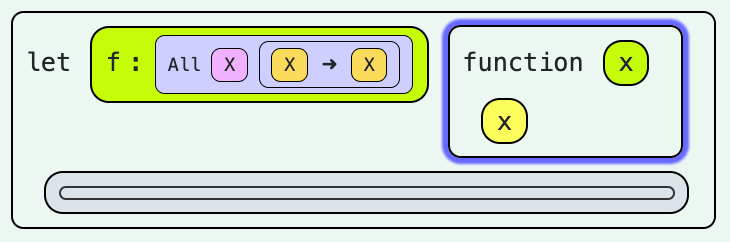
Gradual typing

Gradual typing is the term of art for optional static typechecking with strong guarantees for fully annotated programs. ²

In a gradually typed language, at each point where the type inference algorithm requires a manual annotation, programmers may choose instead to leave parts of their programs statically untyped. In effect, this disables the static typechecker in these parts of the program. But importantly, when programmers choose to fully annotate their programs, gradual type systems provide exactly the same soundness properties as their non-gradual counterparts.

To implement gradual typing, we define a consistent subtyping relation $\lesssim$, which says that $\texttt{T} \lesssim \texttt{U}$ (”$\texttt{T}$ is a consistent subtype of $\texttt{U}$”) iff $\texttt{T}$ and $\texttt{U}$ are related by the subtyping relation where they are both known. [³ § 3–4] That is, the consistent subtyping rules are precisely the subtyping rules with "$<:$" replaced by "$\lesssim$", plus:

• $\texttt{?} \lesssim \texttt{T}$ for every type $\texttt{T}$
• $\texttt{T} \lesssim \texttt{?}$ for every type $\texttt{T}$

Despite the name “consistent subtyping”, this is a weakening of the usual subtyping relation. The name comes from the “type consistency” relation $\sim$, used to define gradual typing without subtyping. [³ § 3]

Whenever no subtyping rules apply (other than reflexivity), $\lesssim$ agrees with $\sim$, which is symmetric:

• $(\texttt{?} \to \texttt{?}) \lesssim \texttt{?}$ — right side has unknown structure, OK;
• $(\texttt{Bool} \to \texttt{?}) \lesssim (\texttt{?} \to \texttt{Integer})$ — matching outer structure, $\texttt{?} \lesssim \texttt{Bool}$, and $\texttt{?} \lesssim \texttt{Integer}$, OK;
• $(\texttt{?} \to \texttt{Integer}) \lesssim (\texttt{Bool} \to \texttt{?})$ — matching outer structure, $\texttt{Bool} \lesssim \texttt{?}$, and $\texttt{Integer} \lesssim \texttt{?}$, OK;
• $(\texttt{Bool} \to \texttt{?}) \textcolor{red}{\not\lesssim} \texttt{Bool}$ — mismatched outer structure, error;
• $(\texttt{Bool} \to \texttt{?}) \textcolor{red}{\not\lesssim} (\texttt{Integer} \to \texttt{?})$ — matching outer structure, but $\texttt{Integer} \textcolor{red}{\not\lesssim} \texttt{Bool}$, error.

When subtyping rules do apply, $\lesssim$ is not symmetric:

• $(\texttt{Number} \to \texttt{?}) \lesssim (\texttt{Integer} \to \texttt{?})$ — matching outer structure, $\texttt{Integer} \lesssim \texttt{Number}$, and return type has unknown structure, OK;
• $(\texttt{Integer} \to \texttt{?}) \textcolor{red}{\not\lesssim} (\texttt{Number} \to \texttt{?})$ — matching outer structure, $\texttt{Number} \textcolor{red}{\not\lesssim} \texttt{Integer}$, error;
• $(\texttt{?} \to \texttt{Integer}) \lesssim (\texttt{?} \to \texttt{Number})$ — matching outer structure, $\texttt{Integer} \lesssim \texttt{Number}$, and parameter type has unknown structure, OK;
• $(\texttt{?} \to \texttt{Number}) \textcolor{red}{\not\lesssim} (\texttt{?} \to \texttt{Integer})$ — matching outer structure, $\texttt{Number} \textcolor{red}{\not\lesssim} \texttt{Integer}$, and parameter type has unknown structure, error.

Note that $\lesssim$ is also not transitive: $(\texttt{Integer} \to \texttt{Bool}) \lesssim \texttt{?}$ and $\texttt{?} \lesssim \texttt{Bool}$, but $(\texttt{Integer} \to \texttt{Bool}) \textcolor{red}{\not\lesssim} \texttt{Bool}$. From this perspective, it is clear how any program can be made to typecheck in a gradual system—by smuggling expressions from one side to the other through $\texttt{?}$.

$\lesssim$ agrees with $<:$ when no $\texttt{?}$s appear on either side (in which case “where they are both known” is everywhere). This is why gradual type systems provide the same type safety guarantees as their non-gradual counterparts when no bindings have the type $\texttt{?}$.

Local type inference

Local type inference is a family of syntax-directed type inference algorithms that are incomplete, but work in the presence of subtyping and impedicative polymorphism. ⁴ In this context, “local” means that expression types are inferred according to the types of neighboring expressions in the syntax tree. Constraints are generated and solved once per node, in bottom-up or top-down order, starting from where type information is available. (If insufficient type information is available, users may be required to provide some type annotations, so that there is somewhere to start.) Types inferred bottom-up are called synthesized, while those inferred top-down are called checked or inherited. ⁵ Local inference algorithms are used industrially, in languages such as Java, Scala, Swift and TypeScript. They are also used for Typed Racket.

Polymorphic type argument inference

Sparkground implements synthesis mode. This provides a typechecking mechanism typical of languages with subtyping; but it also provides type argument inference for polymorphic function applications, provided that types for the function call’s arguments are available.

When the type checker reaches a function application node $(\texttt{f}\ \ \texttt{x}_1\ \ \cdots\ \ \texttt{x}_n)$ in the syntax tree, it synthesizes the node’s type as follows:

• The type of f is synthesized.
• The number of arguments ($n$) is checked against the arity of f, which may be variadic.
• The type of each argument $\texttt{x}_i$ is synthesized.
• A constraint system is generated with the known argument types as lower bounds on f’s parameter types. [⁴ § 3.2–3.3]
• A solution to the constraint system is computed. This will be a minimal solution for the return type R of f, whenever such a solution exists. If no solution is available, a typechecking error is emitted.
• R is instantiated with type arguments according to the constraint system’s solution. This yields the synthesized type for $(\texttt{f}\ \ \texttt{x}_1\ \ \cdots\ \ \texttt{x}_n)$.

Each constraint system consists of subtype constraints and untyped constraints.

Untyped constraints arise when a type with free type variable #X is computed to be bounded above or below by ?. In these cases, the constraint “#X is untyped” enforces that $\texttt{\#X} := \texttt{?}$ is the only correct solution—in effect, #X has been “poisoned” by its untyped context, and forced to also become untyped. This is how gradual typing disables the typechecker in a cascading way. Untyped constraints are straightforward, so we will ignore them from here on.

Subtype constraints look like "$\texttt{L} \lesssim \texttt{\#X} \lesssim \texttt{U}$", expressing that L must be assignable to #X, and #X must be assignable to U. One-sided constraints can be expressed by setting $\texttt{L} = \texttt{Never}$ or $\texttt{U} = \texttt{Any}$.

A solution to the constraint system $\mathcal{S} = \{\, \texttt{L}_i \lesssim \texttt{\#X}_i \lesssim \texttt{U}_i \,\}_{i=1}^m$ is a substitution $\{\, \texttt{\#X}_i := \texttt{T}_i \,\}_{i=1}^m$ such that $\texttt{L}_i \lesssim \texttt{T}_i \lesssim \texttt{U}_i$ for all $i \in [1..m]$. Note that trivial solutions such as $\{\, \texttt{\#X}_i := \texttt{?} \,\}_{i=1}^m$ are “correct”, but not useful; therefore, the constraint solver treats ? as a formal base type, to keep ? usage in computed solutions to a minimum.

A minimal solution to $\mathcal{S}$ for (return type) R is an $\mathcal{S}$-solution $\sigma$ such that $\sigma\texttt{R} <: \tau\texttt{R}$ for every possible $\mathcal{S}$-solution $\tau$. Not every $(\mathcal{S}, \texttt{R})$ pair has a minimal solution—in particular, when R is invariant in a type variable with more than one admissible value. For example, let $\texttt{R} = \texttt{\#X} \to \texttt{\#X}$, and note that $\{\, \texttt{\#X} := \texttt{S} \,\} \texttt{R} <: \{\, \texttt{\#X} := \texttt{T} \,\} \texttt{R}$ only if $\texttt{S} = \texttt{T}$, and thus $\sigma\texttt{R} <: \tau\texttt{R}$ only if $\sigma = \tau$. So whenever multiple (nontrivial) solutions are admissible, none of them are minimal. (If $\mathcal{S} = \{\, \texttt{T} \lesssim \texttt{\#X} \lesssim \texttt{T} \,\}$, there is exactly one nontrivial solution; otherwise there are multiple.) [⁴ §3.5]

The existence of $(\mathcal{S}, \texttt{R})$ pairs with no minimal solution is a well-known problem, with an associated design tradeoff: should the inference of R succeed in such cases (with a solution that may not be minimal), or should it fail? ⁶

Different languages solve this problem in different ways. Typed Racket allows these inferences to succeed, using some appropriate heuristic for whether to resolve R up or down—and it happens to infer the type (-> Any Any) for the return value (λ (x) x). Meanwhile, Scala lets it fail: when given def xToX = x => x, the typechecker complains that it “could not infer type for parameter x of anonymous function”. Proponents of the latter behaviour argue that inference should only succeed when the type it finds is no more general than one the user could have given with a manual annotation. [⁶ § 4.1]

Due to a combination of factors…

• Sparkground is geared toward novices;
• type annotations take up a significant amount of space in the block-based UI;
• adding type annotations in the block-based UI can be a tedious process

…Sparkground works more like Typed Racket than Scala here: whenever R is invariant in a type variable, the variable is resolved to its lower bound. To reiterate, this is a valid solution to the constraint system; at worst, inference chooses an undesirable (but still correct) type for some terms. From empirical observations, such a problem appears rare enough to be acceptable.

Function type synthesis

The type of each lambda abstraction $(\lambda\ \ ((\texttt{x}_1\ : \texttt{T}_1)\ \ \cdots\ \ (\texttt{x}_n : \texttt{T}_n))\ \ \texttt{body})$ is synthesized as follows:

• The current type context is augmented, with the parameters $\texttt{x}_i$ bound to their annotated types $\texttt{T}_i$ (where $\texttt{T}_i = \texttt{?}$ when $\texttt{x}_i$ has no type annotation).
• The type B of body is synthesized under the new type context.
• The overall synthesized type is computed as $(\texttt{T}_1\ \cdots\ \texttt{T}_n \to \texttt{B})$.

Type join and meet

There are two binary operations on types, join $\vee$ and meet $\wedge$. They give us a lattice of types corresponding to the subtyping order—except when ?s are present, which force the result to be ?. These operations are called upon by the constraint generator to combine the lower and upper bounds of multiple subtype constraints. Lower bounds are combined with join $\vee$ and upper bounds with meet $\wedge$. In the final constraint system, each variable will have at most one subtype constraint.

Type join is defined as:

$$\texttt{T} \vee \texttt{U} := \begin{cases} \texttt{?} &\text{if } \texttt{T} = \texttt{?} \text{ or } \texttt{U} = \texttt{?} \\ \texttt{U} &\text{if } \texttt{T} <: \texttt{U} \\ \texttt{T} &\text{if } \texttt{U} <: \texttt{T} \\ \forall\overline{\texttt{\#X}}.\ \texttt{V} \vee \texttt{W} &\text{if } \texttt{T} = \forall\overline{\texttt{\#X}}.\ \texttt{V} \text{ and } \texttt{U} = \forall\overline{\texttt{\#X}}.\ \texttt{W} \\ (\texttt{C}\ \texttt{V}_1\ \cdots\ \texttt{V}_n) &\text{if } \texttt{T} = (\texttt{C}\ \ \texttt{T}_1 \cdots\ \ \texttt{T}_n) \text{ and } \texttt{U} = (\texttt{C}\ \ \texttt{U}_1 \cdots\ \ \texttt{U}_n), \text{ where } \texttt{V}_i = \texttt{T}_i \diamond_{v(\texttt{C}, i)} \texttt{U}_i \\ \texttt{Any} &\text{otherwise}. \end{cases}$$

Type meet is the dual:

$$\texttt{T} \wedge \texttt{U} := \begin{cases} \texttt{?} &\text{if } \texttt{T} = \texttt{?} \text{ or } \texttt{U} = \texttt{?} \\ \texttt{T} &\text{if } \texttt{T} <: \texttt{U} \\ \texttt{U} &\text{if } \texttt{U} <: \texttt{T} \\ \forall\overline{\texttt{\#X}}.\ \texttt{V} \wedge \texttt{W} &\text{if } \texttt{T} = \forall\overline{\texttt{\#X}}.\ \texttt{V} \text{ and } \texttt{U} = \forall\overline{\texttt{\#X}}.\ \texttt{W} \\ (\texttt{C}\ \texttt{V}_1\ \cdots\ \texttt{V}_n) &\text{if } \texttt{T} = (\texttt{C}\ \ \texttt{T}_1 \cdots\ \ \texttt{T}_n) \text{ and } \texttt{U} = (\texttt{C}\ \ \texttt{U}_1 \cdots\ \ \texttt{U}_n), \text{ where } \texttt{V}_i = \texttt{T}_i \diamond_{-v(\texttt{C}, i)} \texttt{U}_i \\ \texttt{Never} &\text{otherwise}. \end{cases}$$

Note that incomparable types $\texttt{T}$ and $\texttt{U}$ created from the same type constructor join elementwise by $\texttt{T} \diamond_s \texttt{U}$, and meet elementwise by $\texttt{T} \diamond_{-s} \texttt{U}$. This reads as the combination of types $\texttt{T}$ and $\texttt{U}$ with respect to variance $s$ (resp. $-s$). The intent is to preserve the direction (join/meet, up/down) when the parameter is covariant, and flip the direction when the parameter is contravariant. Formally,

$$\texttt{T} \diamond_+ \texttt{U} := \texttt{T} \vee \texttt{U}; \\ \texttt{T} \diamond_- \texttt{U} := \texttt{T} \wedge \texttt{U}.$$

$\texttt{T} \diamond_0 \texttt{U}$ is not defined—if a type constructor is invariant in any parameter, its types do not combine elementwise.

Notes and references

Footnotes

1. type expressions ensure that type blocks remain rendered as types by the editor while not in annotation context. They are not currently useful for any other purpose; evaluating one throws an error. ↩

2. J. Siek, “What is Gradual Typing” (2014): https://wphomes.soic.indiana.edu/jsiek/what-is-gradual-typing/ ↩

3. J. Siek and W. Taha, “Gradual Typing for Objects” (2007), European Conference on Object-Oriented Programming: https://doi.org/10.1007%2F978-3-540-73589-2_2 ↩ ↩²

4. B. Pierce and D. Turner, “Local Type Inference” (1999, 2000), ACM Transactions on Programming Languages and Systems, Vol. 22, No. 1: https://doi.org/10.1145/345099.345100 ↩ ↩² ↩³

5. M. Odersky, C. Zenger and M. Zenger, “Colored Local Type Inference” (2001), ACM POPL ‘01: https://doi.org/10.1145/360204.360207 ↩

6. H. Hosoya and B. Pierce, “How Good is Local Type Inference?” (1999): https://doi.org/20.500.14332/7082 ↩ ↩²